Do You Need to Know Linear Algebra for Machine Learning
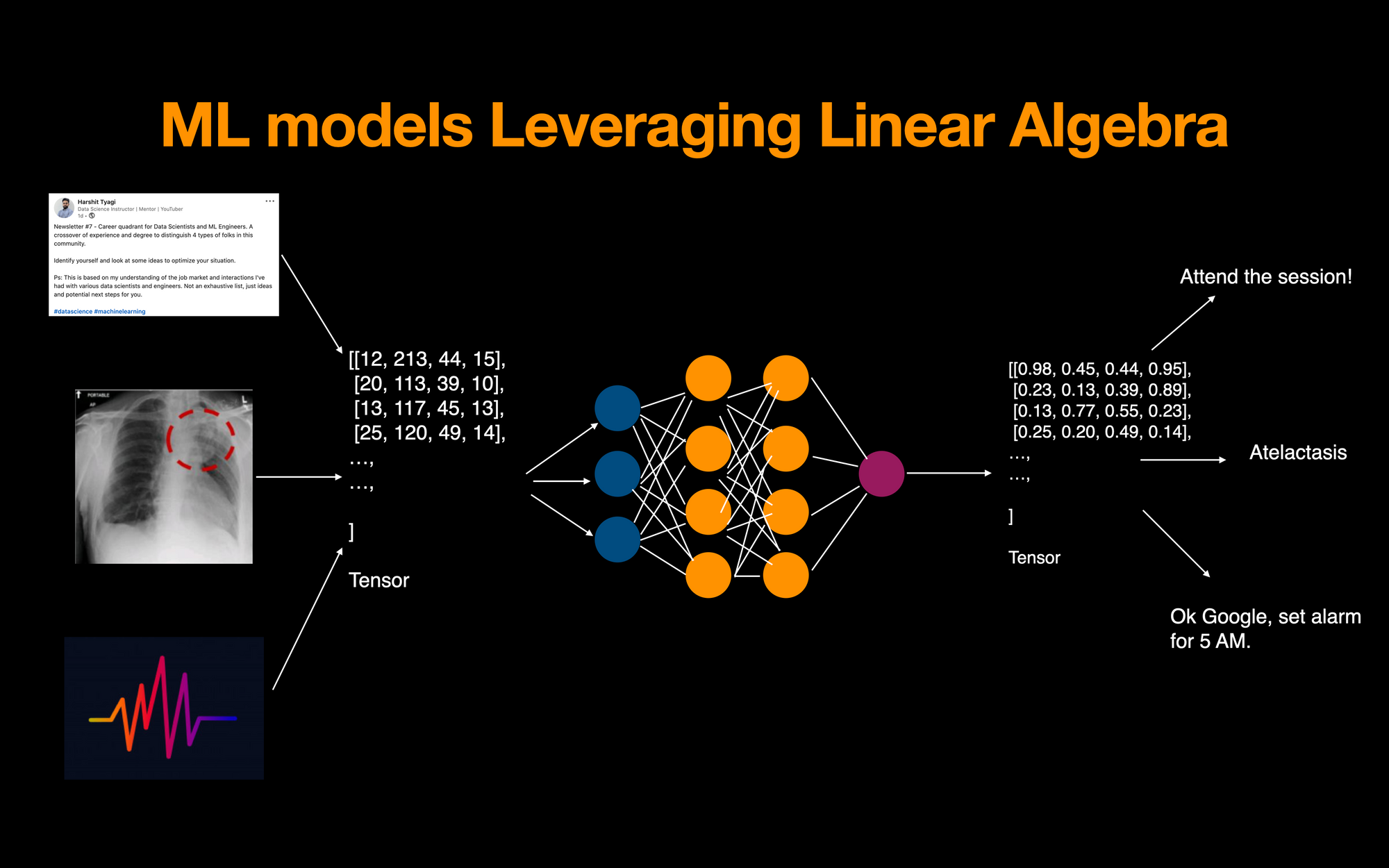
Machines or computers only empathise numbers. And these numbers need to be represented and candy in a way that lets machines solve bug by learning from the information instead of learning from predefined instructions (every bit in the case of programming).
All types of programming use mathematics at some level. Machine learning involves programming information to learn the function that best describes the information.
The problem (or process) of finding the best parameters of a part using information is called model training in ML.
Therefore, in a nutshell, machine learning is programming to optimize for the all-time possible solution – and we need math to empathize how that problem is solved.
The first pace towards learning Math for ML is to learn linear algebra.
Linear Algebra is the mathematical foundation that solves the problem of representing information likewise as computations in machine learning models.
It is the math of arrays — technically referred to every bit vectors, matrices and tensors.
Mutual Areas of Application — Linear Algebra in Action

In the ML context, all major phases of developing a model have linear algebra running backside the scenes.
Important areas of application that are enabled past linear algebra are:
- data and learned model representation
- give-and-take embeddings
- dimensionality reduction
Data Representation
The fuel of ML models, that is data, needs to be converted into arrays earlier you can feed it into your models. The computations performed on these arrays include operations like matrix multiplication (dot product). This further returns the output that is too represented as a transformed matrix/tensor of numbers.
Word embeddings
Don't worry about the terminology here – it is only most representing large-dimensional data (think of a huge number of variables in your data) with a smaller dimensional vector.
Natural Language Processing (NLP) deals with textual information. Dealing with text means comprehending the meaning of a large corpus of words. Each give-and-take represents a different meaning which might be like to another word. Vector embeddings in linear algebra allow us to represent these words more efficiently.
Eigenvectors (SVD)
Finally, concepts like eigenvectors allow us to reduce the number of features or dimensions of the data while keeping the essence of all of them using something called main component analysis.
From Data to Vectors
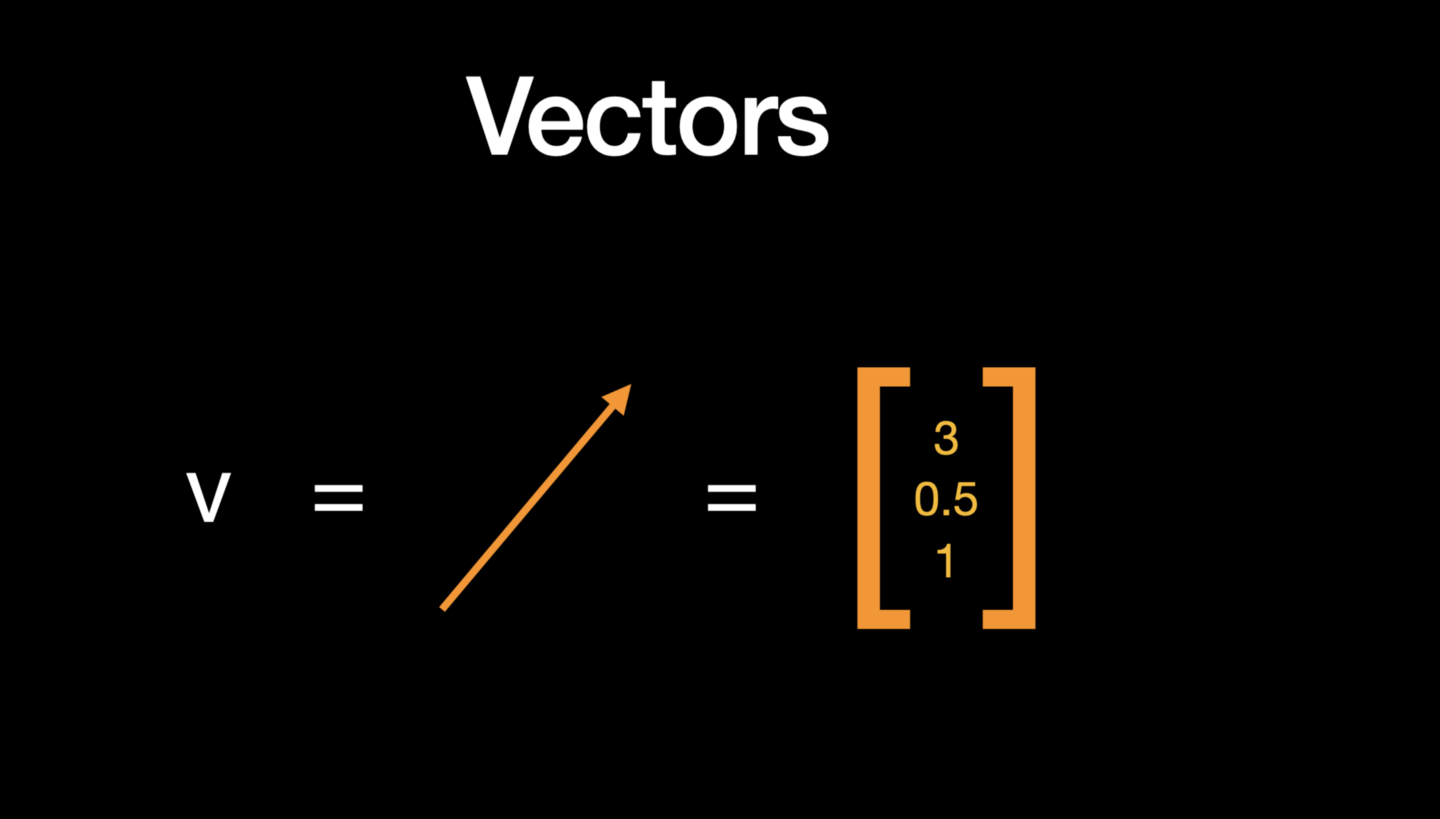
Linear algebra basically deals with vectors and matrices (different shapes of arrays) and operations on these arrays. In NumPy, vectors are basically a 1-dimensional array of numbers but geometrically, they accept both magnitude and direction.
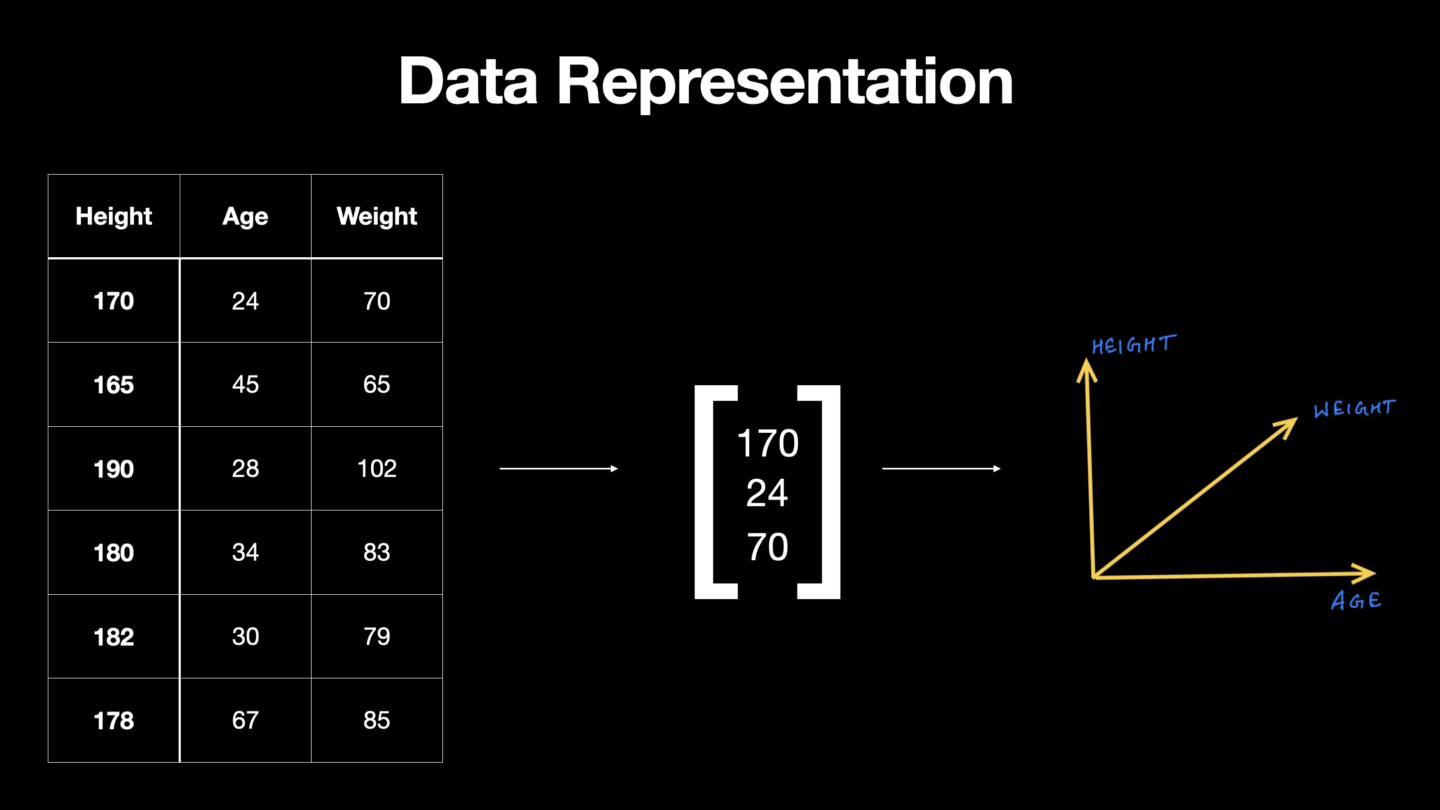
Our information tin be represented using a vector. In the effigy above, i row in this information is represented by a feature vector which has iii elements or components representing iii dissimilar dimensions. North-entries in a vector makes it n-dimensional vector infinite and in this instance, we can come across 3-dimensions.
Deep Learning — Tensors Flowing Through a Neural Network
We can see linear algebra in activity across all the major applications today. Examples include sentiment assay on a LinkedIn or a Twitter post (embeddings), detecting a blazon of lung infection from X-ray images (estimator vision), or any speech to text bot (NLP).
All of these data types are represented by numbers in tensors. We run vectorized operations to learn patterns from them using a neural network. Information technology then outputs a candy tensor which in turn is decoded to produce the terminal inference of the model.
Each phase performs mathematical operations on those data arrays.
Dimensionality Reduction — Vector Infinite Transformation

When information technology comes to embeddings, you lot can basically think of an n-dimensional vector being replaced with another vector that belongs to a lower-dimensional space. This is more meaningful and it'south the i that overcomes computational complexities.
For example, here is a 3-dimensional vector that is replaced by a 2-dimensional space. But yous can extrapolate it to a existent-globe scenario where you have a very large number dimensions.
Reducing dimensions doesn't mean dropping features from the information. Instead, it's about finding new features that are linear functions of the original features and preserving the variance of the original features.
Finding these new variables (features) translates to finding the principal components (PCs). This so converges to solving eigenvectors and eigenvalues problems.
Recommendation Engines — Making use of embeddings
You can think of Embedding equally a second plane existence embedded in a 3D space and that's where this term comes from. Y'all can think of the ground y'all are continuing on as a 2d aeroplane that is embedded into this space in which you live.
Simply to requite you a real-world use case to relate to all of this word on vector embeddings, all applications that are giving yous personalized recommendations are using vector embedding in some form.

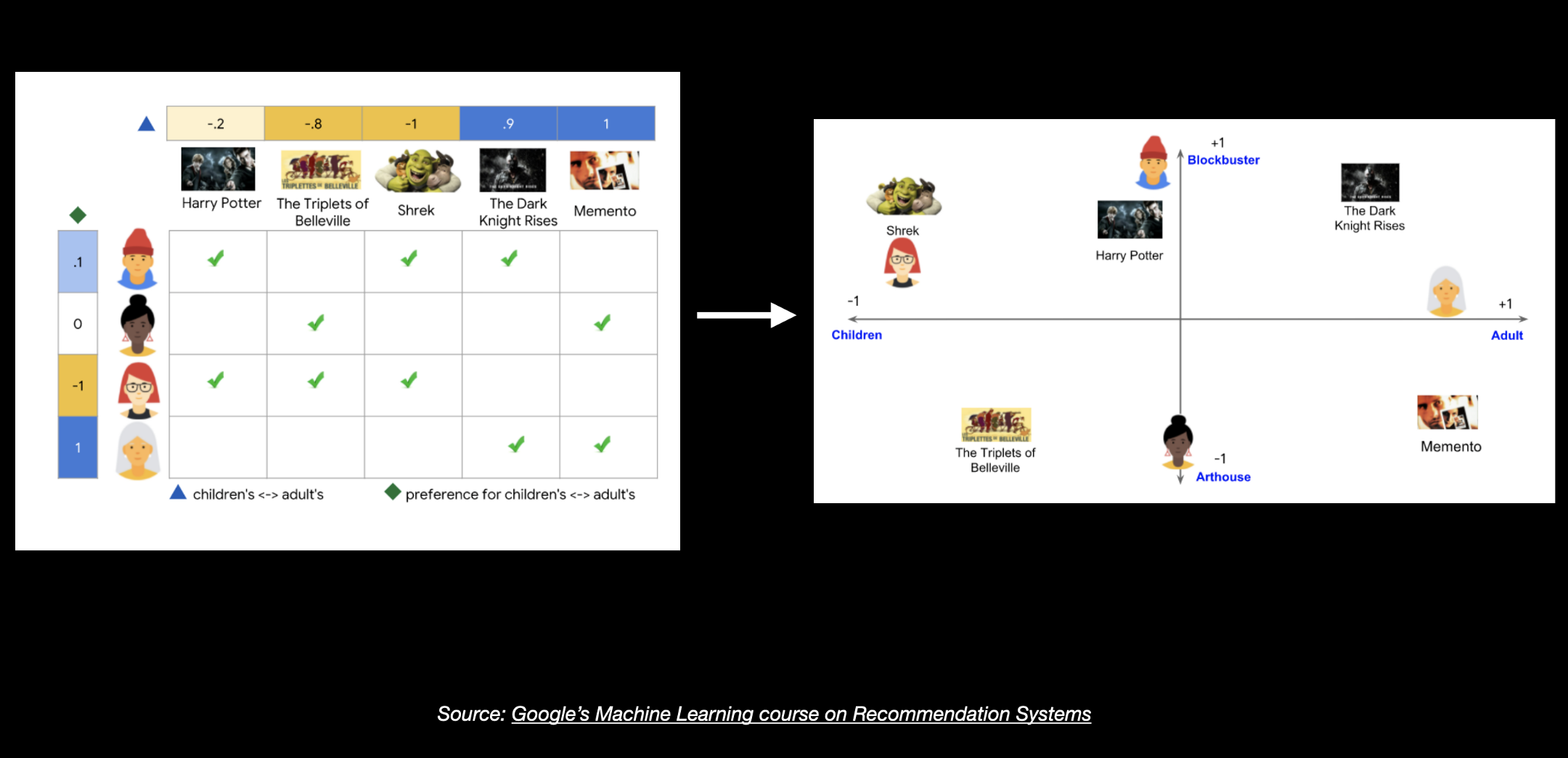
For example, the in a higher place is a graphic from Google's form on recommendation systems where we are given this information on different users and their preferred movies. Some users are kids and others are adults, some movies were are all-fourth dimension classics while others are more artistic. Some movies are targeted towards a younger audience while movies like memento are preferred by adults.
Now, we non just need to represent this information in numbers but also demand to find new smaller dimensional vector representations that capture all these features well.

A very quick way to understand how we can pull off this task is by understanding something called Matrix Factorization which allows united states to interruption a large matrix downwards into smaller matrices.
Ignore the numbers and colors for now and simply endeavor to understand how we have cleaved down ane big matrix into two smaller ones.
For example, here this matrix of 4X5, 4 rows, and 5 features, was cleaved downward into two matrices, 1 that's 4X2 and the other that'southward 2X5. We basically accept new smaller dimensional vectors for users and movies.
And this allows united states of america to plot this on a second vector space. Here you'll see that user #1 and the picture show Harry Potter are closer and user #3 and the motion picture Shrek are closer.
The concept of a dot product (matrix multiplication) of vectors tells the states more about the similarity of two vectors. And it has applications in correlation/covariance calculation, linear regression, logistic regression, PCA, convolutions, PageRank and numerous other algorithms.
Industries where Linear Algebra is used heavily
By now, I promise you are convinced that Linear algebra is driving the ML initiatives in a host of areas today. If not, here is a listing to name a few:
- Statistics
- Chemic Physics
- Genomics
- Word Embeddings — neural networks/deep learning
- Robotics
- Epitome Processing
- Quantum Physics
How much Linear Algebra should you know to become started with ML / DL?
Now, the important question is how yous tin can learn to program these concepts of linear algebra. The answer is you don't have to reinvent the wheel, you but demand to understand the nuts of vector algebra computationally and you then learn to program those concepts using NumPy.
NumPy is a scientific computation packet that gives us access to all the underlying concepts of linear algebra. It is fast equally information technology runs compiled C code and it has a large number of mathematical and scientific functions that we can use.
Recommended resources
- Playlist on Linear Algebra by 3Blue1Brown — very engaging visualizations that explains the essence of linear algebra and its applications. Might be a little too difficult for beginners.
- Book on Deep Learning by Ian Goodfellow & Yoshua Bengio — a fantastic resource for learning ML and applied math. Give it a read, few folks may find it besides technical and notation-heavy, to begin with.
Foundations of Data Science & ML — I have created a course that gives y'all enough understanding of Programming, Math (Basic Algebra, Linear Algebra & Calculus) and Statistics. A complete packet for first steps to learning DS/ML.
👉 You tin can apply the code FREECODECAMP10 to get 10% off.
Check out the class outline here:
Larn to code for gratis. freeCodeCamp's open up source curriculum has helped more than 40,000 people get jobs every bit developers. Go started
wasingerclany1963.blogspot.com
Source: https://www.freecodecamp.org/news/how-machine-learning-leverages-linear-algebra-to-optimize-model-trainingwhy-you-should-learn-the-fundamentals-of-linear-algebra/
0 Response to "Do You Need to Know Linear Algebra for Machine Learning"
Enregistrer un commentaire